부처연구성과
신호처리분야 30년 미해결 난제(가간섭신호문제) 해결
- 등록일2012-01-11
- 조회수7773
-
성과명
신호처리분야 30년 미해결 난제(가간섭신호문제) 해결
-
연구자명
예종철 교수, 김종민 연구교수
-
연구기관
카이스트
-
사업명
중견연구자지원사업(도약연구)
-
지원기관
교육과학기술부, 한국연구재단
-
보도자료발간일
2012-01-11
- 원문링크
-
키워드
#배열신호처리 #압축센싱기술 #가간섭신호문제
- 첨부파일
핵심내용
-의료영상, 무선통신, 스마트 안테나 등 다양한 분야 활용 가능 -
□ 배열신호처리 분야에서 30년간 풀지 못한 문제(서로 간섭하는 신호의 정확한 검출)를 국내 연구진이 해결하였다.
○ 예종철 교수(41세, 카이스트)가 주도하고 김종민 연구교수(제1저자), 이옥균 박사과정생(제2저자) 등이 참여한 이번 연구는 교육과학기술부(장관 이주호)와 한국연구재단(이사장 이승종)이 추진하는 중견연구자지원사업(도약연구)의 지원을 받아 수행되었고, 연구결과는 신호처리 및 정보이론 분야의 권위 있는 학술지인 ‘IEEE Transaction of Information Theory’지 1월호(1월 12일자)에 장문의 논문(24쪽)으로 게재되었다.
(논문명 : Compressive MUSIC : Revisiting the link between compressive sensing and array signal processing)
□ 예종철 교수 연구팀은 최근 신호처리 분야에서 새로운 신호획득 기술로 주목 받고 있는 압축센싱기술*을 이용해 기존의 배열신호처리 기법과 결합된 새로운 신호검출 알고리즘 개발에 성공하였다.
*) 압축센싱(Compressive Sensing) 기술 : 나이퀴스트 (Nyquist) 이론의 한계보다 적은 샘플 수로부터도 완벽하게 신호를 복원할 수 있다는 최신 신호 처리이론
○ 현대의 무선, 의료 및 군용 레이더·센서는 여러 개의 소형 안테나(혹은 센서)를 배열해서 사용하는 경우가 많은데, 이렇게 하면 하나의 큰 안테나와 같은 성능을 얻을 수 있다. 그러나 이때 안테나로 추적하고자 하는 여러 개의 신호원이 동일한 파형이면 서로 간섭을 일으켜 신호원의 위치를 추적할 수 없게 되는데, 이것을 가간섭신호 문제(coherent source problem)라고 한다.
○ 이 문제는 지난 30여 년간 근본적으로 해결되지 못하여, 특히 의료 영상분야의 경우 뇌자도(MEG)와 심자도(MCG) 등을 이용한 간질·심장질환 분석에서도 병변으로부터 나오는 신호가 간섭을 일으키면 정밀한 진단이 불가능하다.
○ 예종철 교수팀은 압축센싱 기술을 이용해 기존의 배열신호처리방법으로 실패한 영역에서 성공할 수 있도록 배열신호처리와 압축센싱을 최적으로 결합할 수 있는 수학적인 조건(Compressive MUSIC algorithm)을 찾아냈다. 그 결과 기존의 배열신호처리 이론과 압축센싱 이론의 장점을 결합하여 지금까지 알고리즘의 한계를 극복할 수 있는 새로운 신호검출 알고리즘을 만들어냈다.
□ 예종철 교수는 “이번 연구결과는 무선통신, 군용레이더 및 의료영상분야 등 센서를 사용하는 모든 분야에 사용되는 원천연구로서 파급효과가 상당히 크다. 특히 국내 바이오공학 분야 연구진들이 IT분야의 난제를 해결했다는 점에서 IT·BT 분야를 아우르는 융합연구의 쾌거라고 할 수 있다”고 연구의의를 밝혔다.
상세내용
연 구 결 과 개 요
배열신호처리(Sensor Array Signal Processing)란 여러 개의 안테나/센서를 이용하여 신호원의 위치를 추정하는 분야로서, 1980년대 무렵 레이더를 이용하여 여러 개의 비행기를 추적하는 군사용 응용으로 개발이 되어왔으며, 그 이후 의료영상, 무선통신, 스마트 안테나 등의 다양한 응용분야에 중요한 신호 검출 이론으로 사용되고 있다.
이때 신호원들의 위치를 추적하는 문제를 그림 1과 같이 나타낼 수 있는데, 이때 신호원들에서 나오는 신호의 간섭이 어느 정도인지에 따라 신호원들의 위치를 추적할 수 있는지의 여부가 결정된다. 즉 그림 1(a)은 신호원들이 시간 축으로 완벽하게 동일한 파형을 가지는 경우인데 이때는 신호원의 위치를 추정하는 것이 불가능하며, 그림 1(c)과 같이 서로 다른 파형을 가지는 경우 가장 추적이 유리하다.
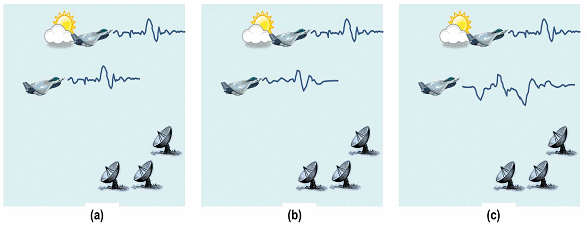
그림 1. 다양한 형태의 신호원들. (a) 신호원의 간섭이 아주 심한 경우 (b) 신호원의 간섭이 조금 있는 경우 (c) 신호원의 간섭이 거의 없는 경우
이러한 배열신호처리 문제는 아래와 같은 수학적인 모델로 설명할 수 있다. 즉, 그림 2에서 행렬 A는 안테나의 감도의 다면체 (Antenna manifold)를 나타내며 B 행렬은 센서에서 얻은 모든 시간에서의 데이터를 특이값 분해 (singular value decomposition) 하여 차원을 줄인 데이터며, 행렬 X는 그에 해당하는 시공간상의 데이터를 의미한다. 가간섭 신호의 경우 그림 2(a)(b)와 같이 시공간의 데이터의 열벡터 개수가 신호원의 수보다 적은 경우를 나타내며, 그림 2(c)는 열벡터의 개수가 신호원의 수보다 많아 서로 간섭을 일으키지 않는 경우를 나타낸다.
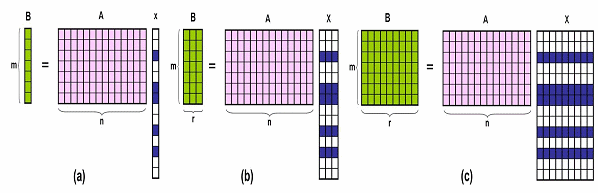
그림 2. 다양한 형태의 배열신호처리 모델 (그림1의 등가 모델)
그림 2(c)의 경우는 배열신호처리에서 널리 사용되는 multiple signal classification (MUSIC) 알고리즘을 적용하면 되지만, 그림 2(a)(b)와 같이 가간섭신호 문제의 경우에서는 rank(B)가 추적하고자하는 신호원의 수보다 작게 되어서 MUSIC 조건이 성립을 하지 않게 되어서 신호원들의 위치를 구할 수 없게 된다.
이러한 문제는 그림 3과 같이 기하학적으로 볼 수 있는데, 여기에서 R(B)는 신호공간, R(Q)는 잡음공간이며 R(AX)는 신호원의 위치 X에 해당하는 부분으로 이루어진 공간이라고 할 때, 가간섭신호의 경우 신호원 위치에 해당하는 안테나 감도의 다면체의 원소가 잡음공간과 직교하지 않는다는 것을 알 수 있다 (점선부분). 하지만 rank(B)와 신호원의 개수의 차에 해당하는 신호의 위치에 대한 정보 를 다른 방식으로 추정할 경우 안테나 감도의 다면체의 원소는 이렇게 합하여 얻어진 부공간의 잡음공간과 직교하는 것을 알 수 있다.
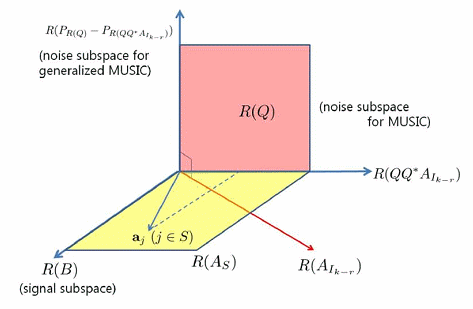
그림 3. 가간섭신호 문제의 기하학적 구조 및 일반화된 MUSIC의 구조
이러한 기하학적인 구조를 이용하면 그림 4와 같이 압축센싱의 기법과 배열신호처리의 기법을 최적으로 결합할 수 있는 있는 일반화된 압축 MUSIC 조건을 얻을 수 있다. 즉, rank(B)와 전체 신호원의 수의 차에 해당하는 신호원의 위치를 압축센싱 기법으로 얻어내고, 나머지에 해당하는 신호원의 위치는 배열신호처리 기법으로 얻어낼 수 있다는 것이다.

그림 4. 압축센싱과 배열신호처리의 최적의 결합을 통한 가간섭신호원 추정기법
이번에 발견된 최적 신호 검출 이론은 단순 명료함에도 불구하고, 지난 30년간 밝혀지지 않았는데, 이는 기존의 연구가 신호처리만을 이용하는 결정적인 방법론과 압축센싱 만을 이용하는 확률적인 방법론의 양극단의 접근법만을 통하여 문제를 해결하려고 하여, 문제의 구조를 근본적으로 이해하지 못한데 있었다는 것이다. 예종철 교수는 “콜럼버스의 달걀과 같은 발상전환을 통하여 양극단의 연구를 최적의 방법으로 통합할 수 있는 기하학적인 구조를 발견하였다”는 것이 연구의 성과라고 강조한다.
용 어 설 명
1. 배열신호처리 (Array Signal Processing)
○ 여러 개의 안테나(또는 센서)를 이용하여 신호원의 위치를 추정하는 분야로서, 1980년대 무렵 레이더를 이용하여 여러 개의 비행기를 추적하는 군사용 응용으로 개발이 되어왔으나, 그 이후 의료영상, 무선통신, 스마트 안테나 등의 다양한 응용분야에도 중요한 신호 검출 이론으로 사용되고 있다.
2. 압축센싱(Compressive Sensing) 기술
○ 신호 획득의 기본 원리인 나이퀴스트 (Nyquist) 한계에서 이야기하는 샘플수보다 훨씬 적은 샘플 수로부터도 완벽하게 신호를 복원 할 수 있다는 혁명적인 최신의 디지털 신호 획득 이론으로 이러한 기법을 바이오 및 의료영상에 적용해 시공간적인 분해능의 한계를 극복하고 초고해상도 영상을 복원할 수 있다.
3. 가간섭신호문제 (Coherent Source Problem)
○ 안테나로 추적하고자 하는 여러 개의 신호원이 시간 축으로 동일한 파형을 가질 경우 서로간의 간섭을 일으켜서, 신호원의 위치를 추적하는 것이 불가능한 문제. 의료 영상분야의 경우 뇌자도(MEG), 뇌전도(EEG) 및 심자도(MCG) 등을 이용한 간질 및 심장질환 분석에 있어서도 병변으로부터 나오는 신호가 간섭을 일으키는 경우, 신호원의 위치에 대한 정밀한 진단이 불가능하다.
4. MUSIC (MUltiple SIgnal Classification)
○ 배열신호처리문제에서 널리 사용되는 방법으로, 안테나(또는 센서)에 측정된 데이터들로 이루어진 공간을 신호 공간과 잡음 공간으로 분리하여 신호원들의 위치에 대한 벡터가 잡음 공간과 직교함을 이용하여 위치를 추적하는 방법이다. 이때에 신호 공간과 잡음 공간을 분리하기 위해서는 신호원들의 시간 축으로의 파형이 간섭이 서로 없어야 한다.
5. CS (Compressive Sensing/Compressed Sensing)
○ 복원하고자 하는 신호가 희소하게 분포할 때에 기존의 현대 디지털 신호처리의 기본 원리인 나이퀴스트 (Nyquist) 한계에서 이야기하는 샘플수보다 훨씬 적은 샘플 수로부터도 완벽하게 신호를 복원 할 수 있다는 혁명적인 최신의 디지털 신호 획득 이론이다.
사 진 설 명
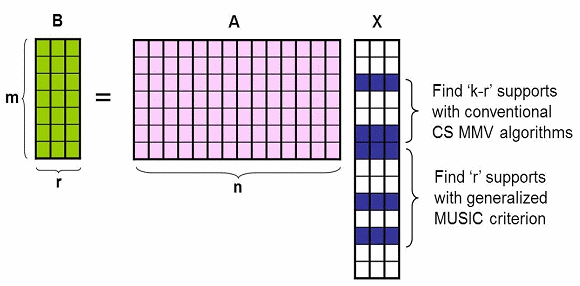
그림 1. Generalized MUSIC 조건을 사용하여 신호원들의 위치를 찾는 과정. 먼저 기존의 CS 복원 알고리즘을 사용하여서 신호원들 중 일부의 위치를 찾고, 이를 바탕으로 나머지 신호원들의 위치를 Generalized MUSIC 조건을 사용하여 찾는다.
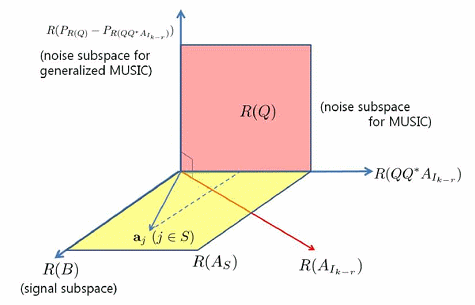
그림 2. 가간섭 문제에서 Generalized MUSIC 조건의 기하학적인 관점. R(B)는 신호공간, R(Q)는 잡음공간이며 R(Ax)는 sensing matrix에서 신호원의 위치 x에 해당하는 부분으로 이루어진 공간을 의미한다. 가간섭 문제이기 때문에 신호원의 위치에 해당하는 sensing matrix 가 잡음공간과 직교하지 않는 반면에(점선부분), Generalized MUSIC 조건에 따라 새롭게 정의된 잡음공간과는 직교하는 것을 알 수 있다.
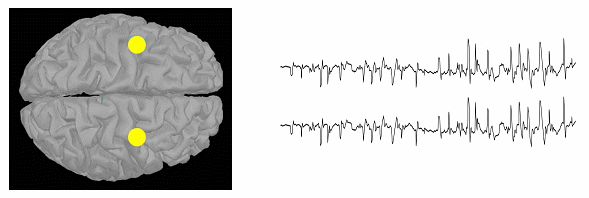
그림 3. 뇌전도(EEG)/뇌자도(MEG)를 이용한 간질 초점 국소화 문제에 있어서의 가간섭 신호원 분리 문제. 두 개의 상이한 간질 초점에서 동일한 발작간극파를 가지는 경우 배열신호처리를 이용한 간질원의 분리가 불가능하다.


 신호처리분야_30년난제해결.hwp
신호처리분야_30년난제해결.hwp